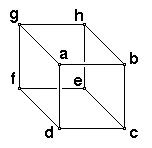
Let's look at the simplest three-dimensional cube.
It connects eight nodes. Every node is connected to three other ones (in the x, y, and z dimension). Starting from any one node, I can reach one in 0 hops (the one I started with, let's say a), three others in 1 hop (b, g, d), three more in the 2nd hop (h, f, c), and the remaining eigth node in a 3rd hop (e); taking 1 1/2 hops to reach any node on average, and 3 in the worst case.
But the Petersen Graph
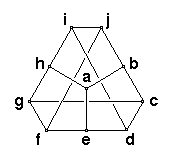
connects more nodes with a better worst-case behavior: reaching one after 0 hops (take, again, a), three after 1 hop (h, b, e), and six more after 2 hops (c, d, f, g, i, j); ten in total. Again, the average hop-count is 1 1/2, but the worst case is only 2.
Does this scale? It doesn't scale to the general case, but to which does it scale?