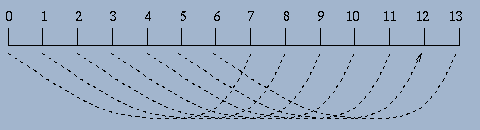
Abbildung: Sieben verschiedene Arten, die Entfernung 7 cm zu messen.
Aufgabe 1 (theoretisch, 1 Punkt)
Wieso hat sich Unix seit Mitte der 70er Jahre so stark an Universitäten
verbreitet?
Wieso gibt es seit ca. 1980 so viele unterschiedliche Varianten?
Welche Hauptentwicklungsrichtungen gibt es?
Wie heißen die beiden Erfinder von Unix und C?
Aufgabe 2 (theoretisch, 2 Punkte)
Erläutert kurz Sinn und Funktionsweise des folgenden ShellSkripts:
#! /bin/sh
case $# in
3) if test -d $2
then files=`find $2 -type f -exec grep -l $3 /dev/null {}\;`
case $1 in
-p) more $files;;
-r) rm -i $files;;
-v) for f in $files
do
vi +/$3 $f
done;;
*) echo 'First argument has to be one of -p, -r or -v!';;
esac
else echo 'Second argument has to be a directory!'
fi;;
*) echo 'Need 3 arguments!';;
esac
Aufgabe 3 (theoretisch, 3 Punkte)
Es gibt in C einige Fallstricke, über die man beim Programmieren leicht stolpern kann. Diese Übung dient dazu, sie (für immer?!) auszumerzen. Also Vorsicht: Viele Fallen!
Welchen Rückgabewert liefert folgende Funktion? Begründe die Antwort!
int f()
{
unsigned int i,k;
k = 0; i = 10;
while (i > 0) {
if (i > 5)
if (i == 5)
k += 10;
else
k++;
i--;
}
return (k);
}
Welche Werte haben die Variablen a, b und c nach dem Ausführen des
folgenden Programmstücks? Begründe die Antwort!
int a = 0, b = 10, c = 4711;
if (a >= b)
if (a > b)
c = 1;
else
c = -1;
while (++b < 20);
a += 1;
Welchen Laufzeitfehler wird das folgende Programm verursachen?
Begründe die Antwort!
#define MAX 80
int buf[MAX];
int i = 1;
for (; i <= MAX;)
buf[i++] = i;
Aufgabe 4 (theoretisch, 1 Punkt)
Die folgende Einleseroutine enthält 3 Fehler. Welche?
#include <stdio.h>
void getline() {
char c;
while (c = getchar() != EOF || c != '\n')
do_something(c);
return;
}
Aufgabe 5 (theoretisch, 3 Punkte)
Gegeben sei:
int a[] = {3, 1, 4, 7, -1, 4711, 815, 9};
int *p;
p = &a[2];
Welchen Wert liefern die folgenden Ausdrücke (expressions),
und auf welches Feldelement von a zeigt der Zeiger p
anschließend, wenn jeweils
vom vorhergehenden Zustand ausgegangen wird?
a) *p b) *p++ c) *p+4 d) *(p+4) e) *++p f) *p+*(p-1)+*(p+1)
Aufgabe 6 (praktisch, 10-30 Punkte)
Von den folgenden drei Aufgaben
muß zum Erreichen der normalen Maximalpunktzahl nur eine bearbeitet werden. Man kann jedoch bei anderen Übungen verlorene Punkte ausgleichen oder sich später eine relativ einfache Aufgabe im 6. Übungsblatt auswählen (oder einfach Spaß haben), wenn man weitere Aufgaben löst.Ihr müßt zunächst eine der drei Aufgaben auswählen und bis zum Abgabetermin fertigstellen. Dafür gibt es dann maximal 10 Punkte. Wollt Ihr auch eine oder beide der anderen Aufgaben bearbeiten, so habt Ihr dafür bis zur zweiten Klausur Zeit. Für jede der zusätzlich bearbeiteten Aufgaben gibt es maximal 7 Punkte.
Eine Besonderheit stellt dabei die Aufgabe 6c (GolombLineale) dar.
Aufgabe 6a: Populationsdynamik auf WaTor
Diese Aufgabe beschäftigt sich mit der Populationsdynamik auf dem Planeten WaTor. WaTor ist ein torusförmiger Planet, der vollständig von Wasser bedeckt ist und von Haien und Fischen bewohnt wird. Die Zeit läuft auf WaTor auf eine besondere Art ab, nämlich in diskreten Schritten, Chrononen genannt. Die Oberfläche des Planeten ist in Felder unterteilt. Ein Feld kann zu einem Zeitpunkt entweder einen Fisch, einen Hai oder einfach nur Wasser enthalten.
Solange sie nicht von einem Hai gefressen werden, schwimmen die Fische ziemlich ziellos umher. Nahrung für sie ist stets im Überfluß vorhanden. Bei jedem neuen Chronon sucht sich jeder Fisch ein zufällig gewähltes Nachbarfeld aus, das nur von Wasser bedeckt ist und bewegt sich dorthin. Ist ein Fisch nun drei Chrononen alt (oder älter, s.u.), entstehen aus ihm zwei neue Fische, die 0 Chrononen alt sind (eine ziemlich seltsame Art der Vermehrung). Der neu hinzugekommene Fisch befindet sich dann auf dem Feld, von dem der alte Fisch herkam. Er geht anschließend seine eigenen Wege. Sind alle vier Nachbarfelder besetzt, bewegt sich der Fisch nicht und vermehrt sich auch nicht.
Das Leben der Haie ist etwas komplizierter. Auch Haie bewegen sich bei jedem Chronon, doch da sie sich natürlich von den Fischen ernähren, wählen sie nicht zufällig ein Nachbarfeld aus, sondern eines, das durch einen Fisch besetzt ist. (Die Betonung liegt auf Fisch, die Haie von WaTor sind keine Kannibalen.) Ist kein Fisch auf den Nachbarfeldern, gelten für den Hai die gleichen Zugregeln wie für Fische. Haie können sich erst nach zehn Chrononen vermehren, das läuft dann genau so ab wie bei den Fischen. Im Gegensatz zu Fischen haben jedoch Haie ein Problem: Da ihre Nahrung eben nicht im Überfluß vorhanden ist, sondern aus den gerade erreichbaren Fischen besteht, können sie u.U. verhungern. Das sieht so aus, daß ein Hai einfach verschwindet, wenn er drei Chrononen lang keinen Fisch gefressen hat.
Eure Aufgabe ist es, die Populationsdynamik von WaTor mit dem Computer zu
simulieren und am Bildschirm sichtbar zu machen.
Wir verwenden dafür keine
echte Grafik, das wäre zu kompliziert, sondern die cursesLibrary.
Das
Terminal stellt dabei die aufgespannte Oberfläche des Planeten dar.
Wasser
wird einfach durch ein Leerzeichen dargestellt, Fische durch einen Punkt und
Haie durch eine Null.
Die aktuelle Zahl von Fischen und Haien wird am unteren
Bildschirmrand zusammen mit der Zahl der vergangenen Chrononen angezeigt.
Der
Bildschirminhalt wird nach jedem Chronon auf den neuesten Stand gebracht.
Wir erinnern uns: Der Planet ist torusförmig, was bedeutet, daß jeder Bewohner, der den Bildschirm verläßt, am gegenüberliegenden Rand erscheint. Die Größe von WaTor beträgt 70x20 Felder. Initial wird die Hälfte der sich dadurch ergebenden Felder mit Fischen besetzt; die Zahl der Haie ist gleich einem Zehntel der Fischzahl. Haie und Fische werden zufällig auf unbesetzten Feldern des Planeten verteilt, wobei ihnen auch gleich ein bestimmtes Alter zugewiesen wird, das zwischen 0 und dem jeweiligen Alter zur Vermehrung liegt. Das soll verhindern, daß sich alle Haie und Fische zum gleichen Chronon vermehren und sich ihre Zahl so plötzlich verdoppelt.
Das Programm läuft in einer Schleife.
Jeder Schleifendurchlauf
repräsentiert ein Chronon auf WaTor.
In der Schleife schwimmen und
vermehren sich zunächst alle Fische, die Haie jagen und vermehren sich
danach.
Dabei darf auch die WINDOWStruktur von curses(3)
manipuliert werden,
da Änderungen erst bei einem refresh()
tatsächlich auf dem Bildschirm erscheinen.
Dies soll am Ende der Schleife geschehen.
Überlegt Euch bitte auch eine sinnvolle Abbruchbedingung
für die Schleife.
Vor dem
endgültigen Verlassen des Programms muß nämlich noch
endwin()
aufgerufen werden, damit curses(3) den alten Zustand
des Terminals wiederherstellt.
Die angegebenen Werte für die initiale Anzahl von Haien und Fischen, die Vermehrungsalter und die maximale Länge des Fastens von Haien sind praxiserprobt und ergeben ein Ökosystem, das sehr stabil ist und scheinbar beliebig lange Bestand hat. Es steht Euch natürlich frei, auch mit anderen Werten zu experimentieren oder das Modell des Ökosystems zu verfeinern. Besonders sinnvoll wäre eine Erweiterung, die beim Programmstart die Größe von WaTor an die Größe des Terminals anpaßt.
Programme, die die cursesLibrary verwenden,
müssen mit -lcurses -ltermcap
gelinkt werden.
Die Musterlösung ist ~unix1/wator.
Aufgabe 6b: Genetische Algorithmen
Das Konzept der genetischen Algorithmen wurde in den 60er Jahren von John M. Holland an der Universität von Michigan entwickelt und hat in der Informatik eine gewisse Bedeutung bei der näherungsweisen Lösung von ansonsten nur schwer oder gar nicht lösbaren Problemen erlangt. Dabei wird eine Menge von zunächst völlig ungeeigneten Lösungen auf ein Problem angesetzt. Neue Lösungen züchtet man durch Verpaaren der besten alten Lösungen und durch kleine Veränderungen in den bestehenden Lösungen (Mutationen). Früher oder später tauchen Lösungen auf, die besser sind als ihre Vorgänger; diese werden dann bevorzugt weitergezüchtet.
In dieser Aufgabe befassen wir uns mit einem sehr einfachen Problem, das aber schon einen recht guten Einblick in die Vorgehensweise bei der Problemlösung durch genetische Algorithmen liefert. Wir stellen uns eine Art UrOzean vor, die Ursuppe, in der eine Zahl primitiver Lebewesen, Eleks genannt, lebt. Die Lebensbedingungen in der Ursuppe sind ständigen (aber periodisch wiederkehrenden) Veränderungen unterworfen, die die Eleks möglichst gut vorhersagen müssen, wenn sie überleben wollen. In unserer Ursuppe werden die sich ändernden Lebensbedingungen durch eine Folge von Nullen und Einsen symbolisiert. Die Chromosomen der Eleks stellen einen endlichen Automaten dar, der auf die Eingaben aus der Ursuppe reagiert und Ausgaben produziert, die ebenfalls aus Nullen und Einsen bestehen. Stimmt nun eine Ausgabe mit der darauffolgenden Eingabe aus der Ursuppe überein, so hat das Elek eine Änderung der Lebensbedingungen korrekt vorhergesagt. Die Eingaben aus der Ursuppe wiederholen sich periodisch (z.B. alle sechs Zyklen). Kann ein Elek eine Folge von einhundert Eingabesymbolen richtig vorhersagen, ist es ein perfekter Hellseher und die Evolution (oder Zucht) der Eleks hat ihren Höhepunkt erreicht.
Wie arbeitet nun der endliche Automat eines jeden Eleks? Ein endlicher Automat besitzt eine endliche Zahl verschiedener Zustände. Ein Eingabesignal bewirkt, daß er in einen anderen Zustand übergeht. Unsere ElekAutomaten erzeugen außerdem bei jeder Eingabe ein Ausgabesymbol. Endliche Automaten lassen sich auf verschiedene Arten darstellen, z.B. als Übergangstabelle oder als Übergangsdiagramm. Die Übergangstabelle für einen endlichen Automaten mit den drei möglichen Zuständen A, B und C, der mit Nullen und Einsen als Signalen arbeitet, paßt gerade in eine Tabelle vom Format drei mal vier. Zu jedem Zustand des Automaten und zu jedem möglichen Eingabesymbol gibt es zwei Einträge. Der erste ist das entsprechende Ausgabesymbol, der zweite der Zustand, in den der Automat übergeht:
Eingabesymbol
0 1
---------------------
A | 1 B | 1 C |
Zustand B | 0 C | 0 B |
C | 1 A | 0 A |
---------------------
Ein Beispiel: Wenn sich der durch diese Tabelle repräsentierte Automat gerade im Zustand C befindet und eine Eins empfängt, so wird er eine Null ausgeben und in den Zustand A übergehen.
Ein Übergangsdiagramm dagegen besteht aus markierten Kreisen, die die möglichen Zustände darstellen, und Pfeilen zwischen diesen Kreisen, die die Zustandsübergänge symbolisieren. Jeder Pfeil ist durch das Eingabesymbol markiert, das den Übergang hervorruft, und durch das dadurch erzeugte Ausgabesymbol. Es gibt noch eine weitere Darstellungsart, die besonders gut zur Repräsentation im Computer geeignet ist. Hierfür wird einfach der umrandete Teil der obigen Übergangstabelle hintereinander in einen eindimensionalen Array geschrieben. Das sieht dann so aus:
1B1C0C0B1A0ADer erste Zustand in diesem Array ist gleichzeitig der Startzustand, mit dem das Elek auf die Ursuppe losgelassen wird.
Wenn nun das eben beschriebene Elek auf eine Ursuppe mit der Eingabefolge
0111000010110 angesetzt wird, reagiert es mit der Ausgabe
1000011001000.
Dabei
gibt jedes Ausgabesymbol an, welche Eingabe das Elek als nächstes
erwartet.
Die Trefferquote in diesem Beispiel liegt bei 50%, ist also nicht
höher als bei einfachem Raten.
Sehr viel besser schneidet es allerdings
ab, wenn die Ursuppe eine sich ständig wiederholende Folge von
010011 liefert.
Man vollziehe dies selbst nach.
Je größer die Zahl der Zustände eines Eleks, desto länger darf die sich wiederholende Sequenz von Eingabesymbolen sein, die irgendwann einmal vorhersagbar ist. So ist für eine Menge von Eleks mit vier Zuständen eine Eingabefolge der Periode vier oder sechs gar kein Problem, während es bei einer Periode der Länge acht schon sehr lange dauern kann, bis ein perfekter Hellseher auftaucht. Mit steigender Zahl der Zustände wird die Zahl der möglichen verschiedenen Eleks immer größer und die Wahrscheinlichkeit immer geringer, daß der perfekte Hellseher schon bald auftritt.
Nun zum Aufbau unseres Programms Ursuppe.
Aufgabe 6c: GolombLineale
Mit einem einfachen Lineal, das 13 Markierungen im Abstand von einem
Zentimeter trägt, kann man bei einmaligem Anlegen genau zwölf
unterschiedliche Entfernungen messen.

Abbildung: Sieben verschiedene Arten, die Entfernung 7 cm zu messen.
Läßt sich dieses simple Gerät so verbessern, daß es mehr Längen zu bestimmen erlaubt als Markierungen vorhanden sind? So ist es in der Tat. Man kann alle bis auf fünf Markierungen entfernen und immer noch zehn Entfernungen messen. Dasselbe geht sogar mit einem Lineal, das nur elf Zentimeter lang ist. Dies ist dann ein GolombLineal.
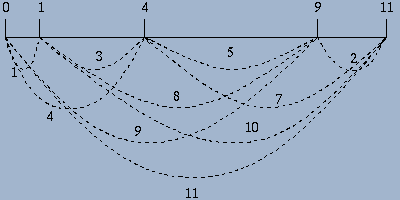
Abbildung: Ein GolombLineal für 10 verschiedene Entfernungen
GolombLineale sind keine bloße mathematische Spielerei. Vielmehr gibt es für sie sehr viele ernsthafte Anwendungen, z.B. in der RöntgenStrukturanalyse, der Chipkonstruktion und der Radioastronomie.
Bevor wir uns der Suche nach solchen Linealen mit Hilfe des Computers widmen, beschäftigen wir uns zunächst mit den Eigenschaften dieser Lineale. Obwohl es unendlich viele dieser Lineale gibt, sind nur die relativ kurzen bekannt. Wir verwenden im folgenden eine sehr einfache Darstellung der Lineale. Um ein Lineal zu beschreiben, das bei 0, 1, 4 und 6 Einheiten jeweils eine Markierung besitzt, schreiben wir 0-1-4-6.
Perfekte GolombLineale sind dadurch charakterisiert, das man mit ihnen jede Entfernung (in ganzen Einheiten) bis zur Gesamtlänge des Lineals messen kann und daß dabei jede Entfernung nur genau einmal vorkommt. So kann man mit einem 6 cm langen Lineal die Entfernungen 1, 2, 3, 4, 5 und 6 cm jeweils genau auf eine Weise messen, wenn man die Markierungen bei 0, 1, 4 und 6 cm anbringt. Die beiden anderen perfekten GolombLineale sind 0-1 und 0-1-3. Man kann beweisen, daß dies die einzigen perfekten GolombLineale sind.
Um weitere Lineale mit ähnlichen Eigenschaften zu finden, muß man also den Anspruch etwas senken. Hiernach ist ein Lineal mit n Markierungen ein (zweitrangiges) GolombLineal, wenn jede damit meßbare Entfernung nur genau einmal vorkommt aber nicht alle Entfernungen zwischen 0 und der Länge des Lineals meßbar sind. Da sich diese Forderung leicht erfüllen läßt, wenn man das Lineal nur lang genug macht, wird noch eine Zusatzbedingung gestellt: Gesucht ist das kürzeste unter allen Linealen mit n Markierungen, die jede Entfernung höchstens einmal abdecken.
Unter anderem sind folgende GolombLineale bekannt:
2: 0-1 3: 0-1-3 4: 0-1-4-6 5: 0-1-4-9-11 6: 0-1-4-10-12-17 7: 0-1-4-10-18-23-25 8: 0-2-12-19-25-30-33-34 9: 0-3-9-17-19-32-39-43-44 10: 0-1-6-10-23-26-34-41-53-55 11: 0-1-9-19-24-31-52-56-58-69-72 12: 0-2-6-24-29-40-43-55-68-75-76-85 13: 0-7-8-17-21-36-47-63-69-81-101-104-106 14: 0-5-28-38-41-49-50-68-75-92-107-121-123-127 15: 0-6-7-15-28-40-51-75-89-92-94-121-131-147-151Die kürzesten bisher bekannten Lineale oberhalb von 15 Markierungen haben die Längen 179, 199, 216, 246, 283, 333, 358, 372 und 425. Bei ihnen ist jedoch mit ziemlicher Sicherheit anzunehmen, daß es noch kürzere gibt. Die Lineale ab vier Markierungen in der obigen Aufstellung sind übrigens zwar die kürzesten aber nicht die einzigen, die es mit der jeweiligen Zahl von Markierungen gibt.
Man kann nun mit Hilfe des Computers die systematische Suche nach solchen Linealen betreiben. Hierfür speichert man in einem das Lineal repräsentierenden Array nicht die Markierungen, sondern die Lücken, wie sie nacheinander zwischen den einzelnen Markierungen auftreten. So hat zum Beispiel ein Lineal mit fünf Markierungen vier Lücken. Der Algorithmus fügt nun ständig neue Zwischenräume dergestalt ein, daß die kürzeste mögliche Lösung nicht überschritten wird.
Er setzt die erste Lücke auf 1 und füllt so lange Einheitslängen in die zweite Lücke, bis sie sich von der ersten unterscheidet. Danach wird die dritte Lücke so lange gefüllt, bis sich nicht nur die Lücken voneinander unterscheiden, sondern auch alle Entfernungen zwischen nicht benachbarten Marken voneinander verschieden sind, usw. Außerdem werden ständig die vorhandenen Lücken aufaddiert und die sich so ergebende Gesamtlänge mit der des kürzesten bekannten Lineals verglichen. Ist sie kleiner (oder gleich) und hat das Lineal bereits die Bedingung der ungleichen Differenzen erfüllt, kann man das gefundene GolombLineal ausgeben und mit der nächstgrößeren Zahl von Markierungen (d.h. mit der nächsten Lücke) fortfahren.
Andernfalls muß man die aktuelle Lücke wieder auf 0 setzen und dann zu der Lücke zurück, die sich vor der aktuellen befindet. Dort vergrößert man nun wieder den Zwischenraum, bis die Bedingung der ungleichen Differenzen erfüllt ist. Wird das Lineal dabei wieder länger als das kürzeste bekannte Lineal, muß man leider noch eine weitere Lücke rückwärts gehen. Handelt es sich bei der aktuellen Lücke um die erste, muß man wieder ganz von vorne beginnen. (Unter strikter Anwendung dieses Algorithmus ist das übrigens spätestens bei einem Lineal mit zehn Markierungen notwendig, was man auch aus der obigen Aufstellung der bekannten Lineale entnehmen kann. Die erste Lücke des Lineals mit zehn Markierungen ist kürzer als die des neunten Lineals, sie muß also irgendwann auf 1 zurückgesetzt worden sein.)
Erfüllt das Lineal nach einem Schritt rückwärts wieder die gewünschten Eigenschaften, kann man wieder zur nächsten Lücke übergehen und dort Zwischenräume einfügen. Das setzt sich fort, bis man bei der aktuell letzten Lücke angelangt ist. Wie man sieht, ist der Algorithmus extrem aufwendig, doch gibt es einige Optimierungen, die zwar nicht die Größenordnung für den Aufwand des Algorithmus verringern, aber doch eine ganze Menge Rechenzeit sparen können. Eine Möglichkeit will ich hier aufzeigen:
Der eigentlich ziemlich aufwendige und nach jeder Vergrößerung einer Lücke notwendige Test, ob alle Entfernungen zwischen nicht benachbarten Marken voneinander verschieden sind (d.h. alle meßbaren Entfernungen höchstens einmal vorkommen) läßt sich so optimieren, daß zunächst ein Array der Länge der maximal möglichen Differenz komplett auf 0 gesetzt wird. Danach läßt man zwei ineinander geschachtelte Schleifen über die Lücken laufen. Die äußere Schleife geht die Lücken nacheinander durch. Wir wollen die gerade durch die äußere Schleife referenzierte Lücke mit A bezeichnen. Die innere Schleife beginnt mit der auf A folgenden Lücke I. Läßt man I bis zum Ende der aktuell betrachteten Lücken laufen und addiert nacheinander die Inhalte der von I referenzierten Lücken, so erhält man jeweils die möglichen Differenzen von A bis zum Ende des Lineals. Jede so ermittelte Differenz dient als Index in den vorbereiteten Array. Ist die gerade ermittelte Differenz noch nicht aufgetreten, so wird an diesem Index noch eine 0 stehen und man trägt dort eine 1 ein. Falls an dem Index schon eine 1 steht, gab es diese Differenz schon einmal und der Test bricht mit einem Mißerfolg ab. Diese Technik gehört zu den Methoden des Hashing, einem Verfahren, das für gewöhnlich dem besonders schnellen Zugriff von in einem Array gespeicherten Werten dient, indem aus einem Suchschlüssel der Index der gesuchten Information im Array direkt berechnet wird. Dadurch entfällt das zeitaufwendige Durchsuchen des Arrays.
Euer Programm soll nacheinander die GolombLineale bis zu 15 Marken berechnen und in geeigneter Form ausgeben können. Da die Berechnung der ersten drei Lineale trivial ist, darf das Programm bei vier Marken beginnen. Die Musterlösung ist ~unix1/golomb. Sie liefert teilweise andere GolombLineale als in der Aufstellung oben, da sie den beschriebenen Algorithmus an einer Stelle etwas abwandelt, um Zeit zu sparen. Überlegt Euch mal, wo.